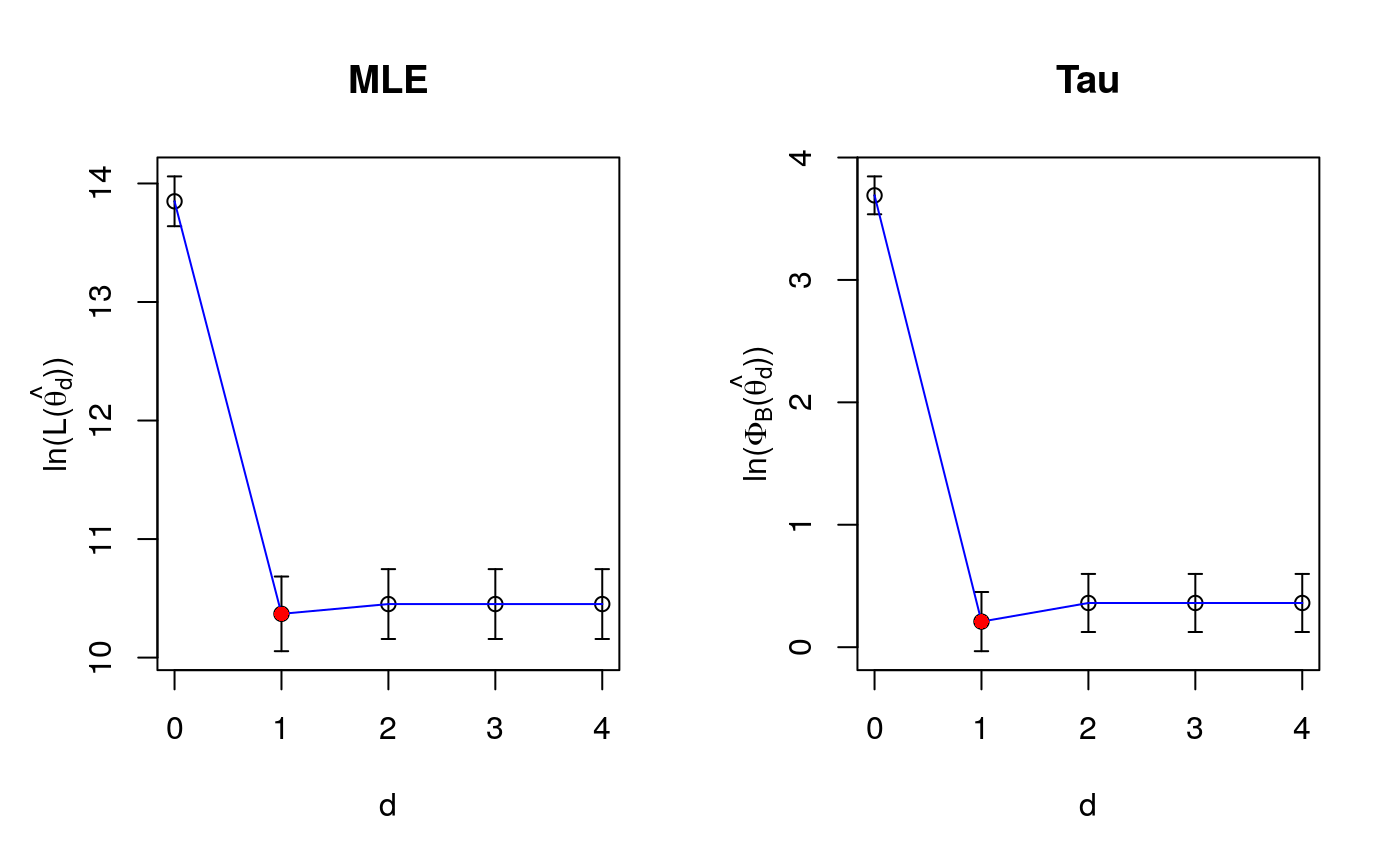
Selection of the dimension of the sufficient reduction subspace

Computes the dimension of the sufficient reduction subspace by cross-validation

cross_val_pfc(X, Fy, dmax, aux, grafico = TRUE)

Arguments

X	vector of response variables in the inverse model
Fy	vector of covariates in the inverse problem, vector containig functions of the response variable in the original problem
dmax	maximum value of the dimension to be evaluated
aux	list containing the constants for the tau-scale
grafico	a logical, if TRUE, shows graphs of the Cross-Validation function versus dimension

Details

The dimension of the reduction subspace, using both maximum likelihood and robust tau estimators to select is computed using five fold cross validation for the PFC model. See Bergesio et al. (2020).

Computes standard deviations of both objective functions and gives back the smaller value that satisfies the one standard deviation rule from the minimum. See Hastie et al. (2009)

Value

List with the following components

d.crossval.ml

dimension selected by cross-validation using ML estimator

obj.ml

objective function values for the ML estimator, for values of d between 0 and dmax

obj.ml.sd

standard deviation of the objective function for the ML estimator, for values of d between 0 and dmax

d.crossval.rob

dimension selected by cross-validation using tau estimator

obj.rob

objective funcion values for the robust estimator

obj.rob.sd

standard deviation of the objective funcion for the robust estimator

...

References

Hastie, T., Tibshirani, R., Friedman, J. H. (2009). The elements of statistical learning: data mining, inference, and prediction. 2nd ed. New York: Springer.

Bergesio, A., Szretter Noste, M. E. and Yohai, V. J. (2020). A robust proposal of estimation for the sufficient dimension reduction problem

Examples

p=10
r=2
n=200
mutrue=rep(0,p)
gamatrue=as.matrix(c(1,rep(0,p-1)))
betatrue=t(as.matrix(c(1,1)))

data_sim=generate(p,n,mutrue,gamatrue,betatrue,sigmatrue=1)
Fy=data_sim$Fy
X=data_sim$X

aux=kappa_and_c(p,efficiency=.9)
cross_val_pfc(X, Fy, dmax=4, aux, grafico=TRUE)
#> $d.crossval.ml
#> [1] 1
#> 
#> $obj.ml
#> [1] 13.84940 10.36917 10.45176 10.45176 10.45176
#> 
#> $obj.ml.sd
#> [1] 0.2100719 0.3148652 0.2947118 0.2947118 0.2947118
#> 
#> $d.crossval.rob
#> [1] 1
#> 
#> $obj.rob
#> [1] 3.6907963 0.2089944 0.3610695 0.3610695 0.3610695
#> 
#> $obj.rob.sd
#> [1] 0.1546360 0.2415973 0.2373233 0.2373233 0.2373233
#>